Topological property

In topology and related areas of mathematics a topological property or topological invariant is a property of a topological space which is invariant under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic to X possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets.

A common problem in topology is to decide whether two topological spaces are homeomorphic or not. To prove that two spaces are not homeomorphic, it is sufficient to find a topological property which is not shared by them.

1 Common topological properties
2 See also
3 References

Common topological properties

Cardinal functions

The cardinality |X| of the space X.
The cardinality τ(X) of the topology of the space X.
Weight w(X), the least cardinality of a basis of the topology of the space X.
Density d(X), the least cardinality of a subset of X whose closure is X.

Separation

For a detailed treatment, see separation axiom. Some of these terms are defined differently in older mathematical literature; see history of the separation axioms.

T₀ or Kolmogorov. A space is Kolmogorov if for every pair of distinct points x and y in the space, there is at least either an open set containing x but not y, or an open set containing y but not x.
T₁ or Fréchet. A space is Fréchet if for every pair of distinct points x and y in the space, there is an open set containing x but not y. (Compare with T₀; here, we are allowed to specify which point will be contained in the open set.) Equivalently, a space is T₁ if all its singletons are closed. T₁ spaces are always T₀.
Sober. A space is sober if every irreducible closed set C has a unique generic point p. In other words, if C is not the (possibly nondisjoint) union of two smaller closed subsets, then there is a p such that the closure of {p} equals C, and p is the only point with this property.
T₂ or Hausdorff. A space is Hausdorff if every two distinct points have disjoint neighbourhoods. T₂ spaces are always T₁.
T_2½ or Urysohn. A space is Urysohn if every two distinct points have disjoint closed neighbourhoods. T_2½ spaces are always T₂.
Regular. A space is regular if whenever C is a closed set and p is a point not in C, then C and p have disjoint neighbourhoods.
T₃ or Regular Hausdorff. A space is regular Hausdorff if it is a regular T₀ space. (A regular space is Hausdorff if and only if it is T₀, so the terminology is consistent.)
Completely regular. A space is completely regular if whenever C is a closed set and p is a point not in C, then C and {p} are separated by a function.
T_3½, Tychonoff, Completely regular Hausdorff or Completely T₃. A Tychonoff space is a completely regular T₀ space. (A completely regular space is Hausdorff if and only if it is T₀, so the terminology is consistent.) Tychonoff spaces are always regular Hausdorff.
Normal. A space is normal if any two disjoint closed sets have disjoint neighbourhoods. Normal spaces admit partitions of unity.
T₄ or Normal Hausdorff. A normal space is Hausdorff if and only if it is T₁. Normal Hausdorff spaces are always Tychonoff.
Completely normal. A space is completely normal if any two separated sets have disjoint neighbourhoods.
T₅ or Completely normal Hausdorff. A completely normal space is Hausdorff if and only if it is T₁. Completely normal Hausdorff spaces are always normal Hausdorff.
Perfectly normal. A space is perfectly normal if any two disjoint closed sets are precisely separated by a function. A perfectly normal space must also be completely normal.
Perfectly normal Hausdorff, or perfectly T₄. A space is perfectly normal Hausdorff, if it is both perfectly normal and T₁. A perfectly normal Hausdorff space must also be completely normal Hausdorff.
Discrete space. A space is discrete if all of its points are completely isolated, i.e. if any subset is open.

Countability conditions

Separable. A space is separable if it has a countable dense subset.
Lindelöf. A space is Lindelöf if every open cover has a countable subcover.
First-countable. A space is first-countable if every point has a countable local base.
Second-countable. A space is second-countable if it has a countable base for its topology. Second-countable spaces are always separable, first-countable and Lindelöf.

Connectedness

Connected. A space is connected if it is not the union of a pair of disjoint non-empty open sets. Equivalently, a space is connected if the only clopen sets are the empty set and itself.
Locally connected. A space is locally connected if every point has a local base consisting of connected sets.
Totally disconnected. A space is totally disconnected if it has no connected subset with more than one point.
Path-connected. A space X is path-connected if for every two points x, y in X, there is a path p from x to y, i.e., a continuous map p: [0,1] → X with p(0) = x and p(1) = y. Path-connected spaces are always connected.
Locally path-connected. A space is locally path-connected if every point has a local base consisting of path-connected sets. A locally path-connected space is connected if and only if it is path-connected.
Simply connected. A space X is simply connected if it is path-connected and every continuous map f: S¹ → X is homotopic to a constant map.
Locally simply connected. A space X is locally simply connected if every point x in X has a local base of neighborhoods U that is simply connected.
Semi-locally simply connected. A space X is semi-locally simply connected if every point has a local base of neighborhoods U such that every loop in U is contractible in X. Semi-local simple connectivity, a strictly weaker condition than local simple connectivity, is a necessary condition for the existence of a universal cover.
Contractible. A space X is contractible if the identity map on X is homotopic to a constant map. Contractible spaces are always simply connected.
Hyper-connected. A space is hyper-connected if no two non-empty open sets are disjoint. Every hyper-connected space is connected.
Ultra-connected. A space is ultra-connected if no two non-empty closed sets are disjoint. Every ultra-connected space is path-connected.
Indiscrete or trivial. A space is indiscrete if the only open sets are the empty set and itself. Such a space is said to have the trivial topology.

Compactness

Compact. A space is compact if every open cover has a finite subcover. Some authors call these spaces quasicompact and reserve compact for Hausdorff spaces where every open cover has finite subcover. Compact spaces are always Lindelöf and paracompact. Compact Hausdorff spaces are therefore normal.
Sequentially compact. A space is sequentially compact if every sequence has a convergent subsequence.
Countably compact. A space is countably compact if every countable open cover has a finite subcover.
Pseudocompact. A space is pseudocompact if every continuous real-valued function on the space is bounded.
σ-compact. A space is σ-compact if it is the union of countably many compact subsets.
Paracompact. A space is paracompact if every open cover has an open locally finite refinement. Paracompact Hausdorff spaces are normal.
Locally compact. A space is locally compact if every point has a local base consisting of compact neighbourhoods. Slightly different definitions are also used. Locally compact Hausdorff spaces are always Tychonoff.
Ultraconnected compact. In an ultra-connected compact space X every open cover must contain X itself. Non-empty ultra-connected compact spaces have a largest proper open subset called a monolith.

Metrizability

Metrizable. A space is metrizable if it is homeomorphic to a metric space. Metrizable spaces are always Hausdorff and paracompact (and hence normal and Tychonoff), and first-countable.
Polish. A space is called Polish if it is metrizable with a separable and complete metric.
Locally metrizable. A space is locally metrizable if every point has a metrizable neighbourhood.

Miscellaneous

Baire space. A space X is a Baire space if it is not meagre in itself. Equivalently, X is a Baire space if the intersection of countably many dense open sets is dense.
Homogeneous. A space X is homogeneous if for every x and y in X there is a homeomorphism f : X → X such that f(x) = y. Intuitively speaking, this means that the space looks the same at every point. All topological groups are homogeneous.
Finitely generated or Alexandrov. A space X is Alexandrov if arbitrary intersections of open sets in X are open, or equivalently if arbitrary unions of closed sets are closed. These are precisely the finitely generated members of the category of topological spaces and continuous maps.
Zero-dimensional. A space is zero-dimensional if it has a base of clopen sets. These are precisely the spaces with a small inductive dimension of 0.
Almost discrete. A space is almost discrete if every open set is closed (hence clopen). The almost discrete spaces are precisely the finitely generated zero-dimensional spaces.
Boolean. A space is Boolean if it is zero-dimensional, compact and Hausdorff (equivalently, totally disconnected, compact and Hausdorff). These are precisely the spaces that are homeomorphic to the Stone spaces of Boolean algebras.
Reidemeister torsion
$\kappa$ -resolvable. A space is said to be κ-resolvable (respectively: almost κ-resolvable) if it contains κ dense sets that are pairwise disjoint (respectively: almost disjoint over the ideal of nowhere dense subsets). If the space is not $\kappa$ -resolvable then it is called $\kappa$ -irresolvable.
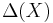Maximally resolvable. Space $X$ is maximally resolvable if it is $\Delta(X)$ -resolvable, where 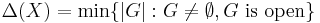$\Delta(X) = \min\{|G|�: G\neq\emptyset, G\mbox{ is open}\}$ . Number 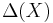$\Delta(X)$ is called dispersion character of $X$ .
Strongly discrete. Set $D$ is strongly discrete subset of the space $X$ if the points in $D$ may be separated by pairwise disjoint neighborhoods. Space $X$ is said to be strongly discrete if every non-isolated point of $X$ is the accumulation point of some strongly discrete set.

References

Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts.
I. Juhasz, L. Soukup, Z. Szentmiklossy, Resolvability and monotone normality.